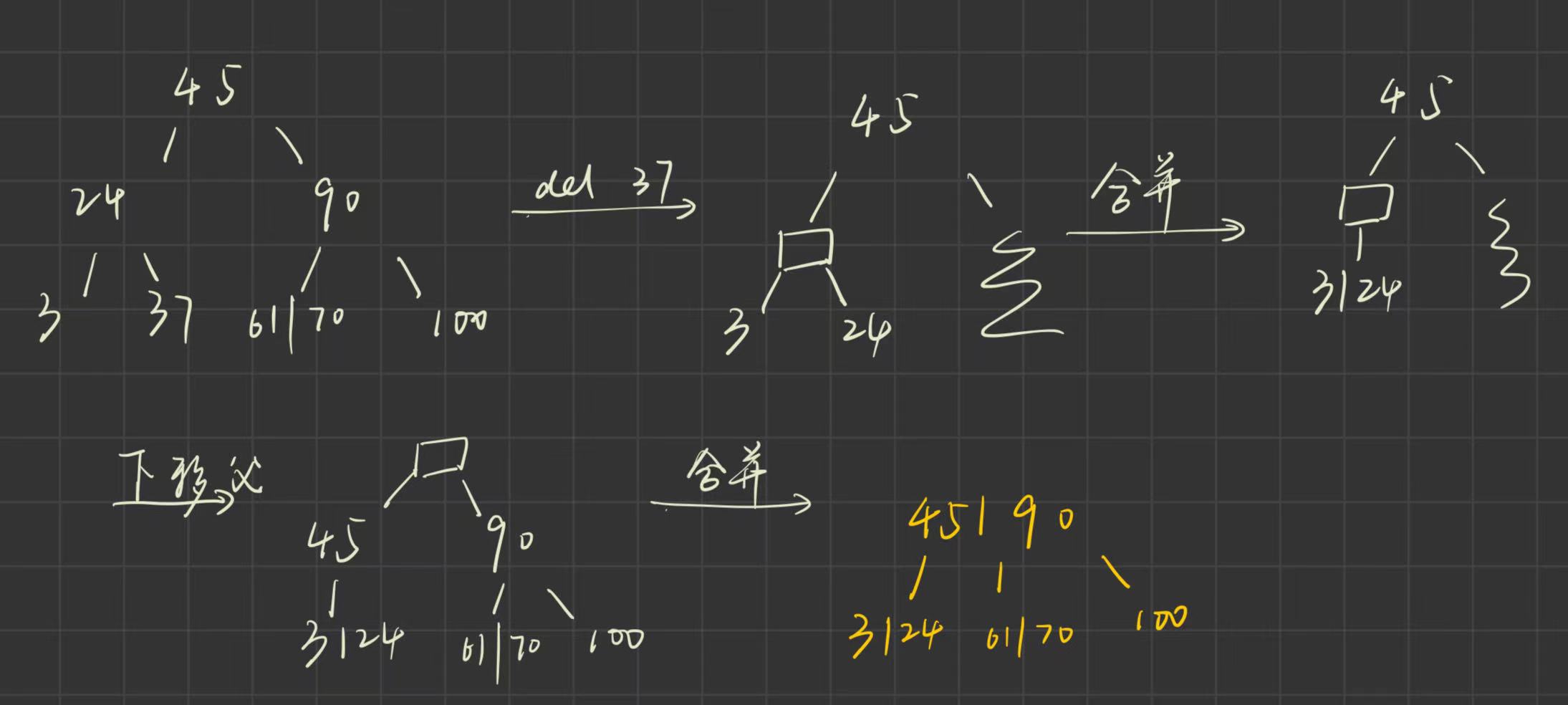链表栈队

链表操作

有序链表的合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
void AddNode(List &list,int data)
{
  Node*newnode=new Node;
  newnode->next=NULL;
  newnode->data=data;
  Node*cur=list;
  while(cur->next!=NULL)
  {
      cur=cur->next;
  }
  cur->next=newnode;
  return;
}

List MergeList(List &listA,List &listB)
{
  List listC;
  InitList(listC); // 初始化合并后的链表

  Node*curA=listA->next;
  Node*curB=listB->next;

  while(curA!=NULL&&curB!=NULL)
  {
      if(curA->data>=curB->data)
      {
          AddNode(listC,curB->data);
          curB=curB->next;
      }
      else if(curA->data<curB->data)
      {
          AddNode(listC,curA->data);
          curA=curA->next;
      }
  }

  while(curA!=NULL)
  {
      AddNode(listC,curA->data);
      curA=curA->next;
  }
  while(curB!=NULL)
  {
      AddNode(listC,curB->data);
      curB=curB->next;
  }

  return listC;
}

查找链表倒数第k个数据（快慢指针）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/*查找倒数第m个节点*/
Node* FindMthNode(const List& list, int m){
Node* p1 = list;
Node* p2 = list;

// 让p2指针向后移动m-1步
for(int i = 0; i < m-1; i++){
  if(p2 == NULL) return NULL;  // 如果链表长度小于m，返回NULL
  p2 = p2->next;
}

// 同时移动p1和p2指针，直到p2指向链表的最后一个节点
while(p2->next != NULL){
  p1 = p1->next;
  p2 = p2->next;
}

return p1;
}

链表的反转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/*头节点也要记得初始化*/
int InitList(List &list){
list=new Node;
list->next=NULL;
return 0;
}

int DestroyList(List &list){
  Node* cur = list;
  while (cur != NULL) {
     Node* temp = cur;
     cur = cur->next;
     delete temp;
  }
  list = NULL;
  return 0;
}

int AddNode(List &list, int data){
  Node*newnode=new Node;
  newnode->next=NULL;
  newnode->data=data;
  Node*cur=list;
  while(cur->next!=NULL)
  {
     cur=cur->next;
  }
  cur->next=newnode;
  return 0;
}

>/*链表反转*/
void ReverseList(List &list){
  Node*cur=list->next;
  Node*prev=NULL;
  while(cur!=NULL)
  {
     Node*next=cur->next;
     cur->next=prev;
     prev=cur;
     cur=next;
  }
  list->next=prev;
}

括号匹配

最最最基础的括号匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <iostream>
#include <string>
using namespace std;
struct Node{
char data;
Node* next;
};
typedef Node* Stack;

void InitStack(Stack& S) {
   // TODO: Initialize the stack.
   S=new Node;
   S->next=NULL;
   return;
}
void DestroyStack(Stack& S) {
   // TODO: Destroy the stack and free all nodes.
   Node*cur=S;
   while(cur!=NULL)
   {
       Node*tmp=cur;
       cur=cur->next;
       delete tmp;
   }
   S=NULL;
   return ;
}

void Push(Stack& S, char data) {
   // TODO: Push an element onto the stack.
   Node*newnode= new Node;
   newnode->data=data;
   newnode->next=S->next;
   S->next=newnode;
   return;
}

bool IsEmpty(const Stack& S) {
   return S == nullptr;  // This check is preserved as it's non-functional.
}

char Pop(Stack& S) {
   if (IsEmpty(S)) {
       return '\0';  // Return null character if stack is empty.
   }
   // TODO: Pop an element from the stack.
   else{
       Node*tmp=S->next;
       S->next=tmp->next;
       delete tmp;
   }
   return '\0';  // Return the popped element or null character.
>}

bool isMatching(const string& str) {
   Stack S;
   InitStack(S);
   for (char c : str) {
       // TODO: Process each character based on the given conditions.
       if(c=='(')
       Push(S,c);

       else{
           if(S->next!=NULL){
               Pop(S);
           }

           else{
               return false;//条件一：输入）时占栈不为空
           }
       }
}

bool result = IsEmpty(S->next);  // 条件二：字符串输入完成后后栈为空
   DestroyStack(S);
   return result;
}

void BracketMatch() {
   string line;
   while (getline(cin, line)) 
   {
       if(isMatching(line))
       {	
           cout<<"YES"<<endl;
       }
       else{
           cout<<"NO"<<endl;
           }
   }
}

int main() {
BracketMatch();
return 0;
}

约瑟夫问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
using namespace std;
using namespace std;
int main()
{
     queue<int> q;
     int n,m;
     int num[10000];
     while(cin>>n>>m)
     {
         cout<<endl;
         for(int i=0;i<n;i++)
         {
             num[i]=i+1;
             q.push(num[i]);
         }

         while(!q.empty())
         {
             for(int i =0;i<m;i++){
                 int x=q.front();

                 if(i==m-1){
                     q.pop();
                     cout<<x<<" ";
                 }
                 else{
                     q.pop();
                     q.push(x);
                 }
             }
         }
     }
}

运算表达式

中缀表达式：建立两个栈

img

后缀表达式：建立一个栈

遇到数字放入栈中，如果遇到操作符则出栈两个数。

中缀转后缀：假设括号，将操作符移动到括号右侧。

杨辉三角

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
void YangHuiTriangle(int N)
{
 int n, i, x, temp;
 queue<int> Q;
 Q.push(1);
 for (n = 2; n <= N; n++)
 {
     Q.push(1);
     for (i = 1; i <= n - 2; i++)
     {
         temp = Q.front();
         Q.pop();
         cout << temp << " ";
         x = Q.front();
         temp = temp + x;
         Q.push(temp);
     }
     x = Q.front();
     Q.pop();
     cout << x << " ";
     Q.push(1);
     cout << endl;
 }
 while (!Q.empty())
 {
     x = Q.front();
     Q.pop();
     cout << x << " ";
 }
}

int main()
{
 int N;
 cout << "please input the N:";
 cin >> N;
 YangHuiTriangle(N);
 cout << endl;
 return 0;
}

KMP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<bits/stdc++.h>
using namespace std;

void GetNext(char str[],int next[])
{
     next[0]=-1;
     next[1]=0;//确定next数组中的前两位。
     int n=strlen(str);
     int x,y;//x用来标记坐标，y用来遍历
     for(int y=1;y<n;y++){
         x=next[y];
         while(str[x]!=str[y]&&x!=-1)//往前面找，如果没有匹配位置则回到x=-1但也不能太往前
         {
             x=next[x];
         }
         next[y+1]=x+1;
     }
     //不断去循环佐证x的位置，最后把值献给y+1
}

void GetNextVal(char str[],int next[],int nextval[])
{
     int i=0;
     nextval[0]=-1;
     int n=strlen(str);
     for(i=1;i<n;i++){
         int j=next[i];
         while(str[i]==str[j]&&j!=-1){
             j=next[j];
         }
         nextval[i]=j;
     }
}

int main()
{
     char str[1000];
     int next[1000];
     int nextval[1000];
     while(cin>>str) {
         int n=strlen(str);
         GetNext(str,next);
         GetNextVal(str,next,nextva	l);
         for(int i=0;i<n;i++){
             cout<<next[i]<<" ";
         }
         cout<<endl;
         for(int i=0;i<n;i++){
             cout<<nextval[i]<<" ";
         }
         cout<<endl;
     }
     return 0;
}

稀疏矩阵

三元组法快速转置矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
#include <iostream>
using namespace std;

struct TriNode
{
int row, col;
int data;
};
struct TriTable
{
 TriNode *datas;
 int mu, nu, tu;  // 行数，列数，非零元个数
};

int CreateTriTable(TriTable &T, int matrix[], int m, int n)
{
 T.mu = m;
 T.nu = n;

 // 统计非零元的个数，分配存储空间
 int count = 0;
 for (int i = 0; i < m*n; i++)
     if (matrix[i] != 0) count++;
 T.tu = count;
 T.datas = new TriNode[count];

 // 填写三元组表
 int k = 0, t = 0;
 for (int i = 0; i<m; i++)
 for (int j = 0; j < n; j++)
 {
 if (matrix[k] != 0)
 {
 T.datas[t].row = i;
 T.datas[t].col = j;
 T.datas[t].data = matrix[k];
 t++;
 }
 k++;
 }
 return 0;
}

int DestroyTriTable(TriTable &T)
{
 delete[]T.datas;
 T.mu = T.nu = T.tu = 0;
 return 0;
}

int PrintTriTable(TriTable &T)
{
 cout << "mu = " << T.mu << ", nu = " << T.nu << ", tu = " << T.tu << endl;
 for (int i = 0; i < T.tu; i++)
     cout << "(" << T.datas[i].row << ", " << T.datas[i].col << ") = " 
         << T.datas[i].data << endl;
 return 0;
}

/*将三元组表结构的矩阵A转置到B*/
int FastTranspose(TriTable &B, TriTable &A)
{
 // 初始化结果三元组表
 B.mu = A.nu;
 B.nu = A.mu;
 B.tu = A.tu;
 B.datas = new TriNode[B.tu];

 // 统计结果矩阵每行非零元个数
 int *rsum = new int[B.mu];
 for (int i = 0; i < B.mu; i++) rsum[i] = 0;
 for (int i = 0; i < A.tu; i++)
     rsum[A.datas[i].col]++;

/*新开数组的大小与转置矩阵的行数相同*/

/*位置数组的大小与三元组的数量有关*/

 // 计算结果矩阵各行在三元组表中的起始下标
 int *rpos = new int[B.mu];
 rpos[0] = 0;
 for (int i = 1; i < B.mu; i++)
     rpos[i] = rpos[i - 1] + rsum[i - 1];

 // 将源三元组表转置到目标三元组表中
 for (int i = 0; i < A.tu; i++)
 {
     int j = rpos[A.datas[i].col];
     B.datas[j].row = A.datas[i].col;
     B.datas[j].col = A.datas[i].row;
     B.datas[j].data = A.datas[i].data;
     rpos[A.datas[i].col]++;
 }
     delete[]rpos;
     delete[]rsum;
 return 0;
}

int main()
{
 int *matrix, m, n;
 cout << "请输入行数 列数：";
 cin >> m >> n;
 matrix = new int[m*n];
 cout << "请按行优先顺序输入矩阵：";
 for (int i = 0; i < m*n; i++)
     cin >> matrix[i];

 TriTable T1;
 CreateTriTable(T1, matrix, m, n);
 cout << "源矩阵：" << endl;
 PrintTriTable(T1);

 TriTable T2;
 FastTranspose(T2, T1);
 cout << "转置后矩阵：" << endl;
 PrintTriTable(T2);

 DestroyTriTable(T1);
 DestroyTriTable(T2);
 delete []matrix;
 return 0;
}

高维下标转换

img

树

树的概念与结论

分类

  • 满二叉树：

    每一层的节点都达到了最大值，如果有k层。那么最多有2**k-1个节点。

  • 完全二叉树

    前k-1层是满的，最后一层从左到右是连续的。高度为h的完全二叉树节点范围是【2^(h-1), 2^h-1】,最后一层最少一个。

小结论

  • 任意一个二叉树，如果度为0的节点有n0个，度为2的节点有n2个。那么n0=n2+1。
  • 完全二叉树，n1要么为0要么为1。
  • 不存在度大于二的节点

  • 物理存储的下标关系：

  • parent=(child-1)/2 两个孩子算出来的整数部分都是相同的

  • leftchild=parent*2+1

  • rightchild=parent*2+2

树的基础操作

树的初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<bits/stdc++.h>
using namespace std;
typedef struct Node
{
 char data;
 Node*lchild;
 Node*rchild;
}Node,*BiTree;

/*初始化树*/
void InitTree(BiTree&tree)
{
tree=NULL;
}

树的前序输入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/*读取结点数据*/
char* GetTree(BiTree&tree,char*str)
{
//如果带存入的数据为空，则将该节点置空，数组下标移到下一个
if('#'==*str)
{
  tree=NULL;
  return str+1;
}
//如果存入数据不为空，新建结点存入数据
tree=new Node;
tree->data=*str;
char*afterleft=GetTree(tree->lchild,str+1);//顺着左侧结点继续输入
char*afterright=GetTree(tree->rchild,afterleft);
return afterright;
}

销毁一棵树

1
2
3
4
5
6
7
8
9
10
/*删除一棵树*/
void DestroyBiTree(BiTree& tree)
{
 if (tree != NULL) {
     DestroyBiTree(tree->lchild); // 递归删除左子树
     DestroyBiTree(tree->rchild); // 递归删除右子树
     delete tree; // 删除当前节点
     tree = NULL;
 }
}

树的四种遍历

递归版本

前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void Leveltraverse(Tree&tree)
{
 //先引入头结点
 queue<Tree>q;
 Tree p=tree;
 q.push(p);
 //判断队列是否为空
 while(!q.empty())
 {
     Tree tmp=q.front();
     q.pop();
     cout<<tmp->data<<"";
     //入队两个新节点
     if(tmp->leftchild)q.push(tmp->leftchild);
     if(tmp->rightchild)q.push(tmp->rightchild);
 }
}

中序遍历

略略略~

后续遍历

略略略~

非递归版本

前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/*查找到最左结点，为空转为找右节点*/
void Pretraverse(Tree&tree)
{
 stack<Tree>s;
 Tree p=tree;
 while(!s.empty()||p!=NULL)
 {
     while(p!=NULL)
     {
         cout<<p->data<<"";

         s.push(p);
         p=p->leftchild;
     }
     if(!s.empty())
     {
         Tree tmp=s.top();
         s.pop();
         p=tmp->rightchild;
     }
 }
}

中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/*和前序类似，只是改变数据结点数据的条件与位置*/
void Intraverse(Tree&tree)
{
 stack<Tree>s;
 Tree p=tree;
 while(!s.empty()||p!=NULL)
 {
     while(p!=NULL)
     {
         s.push(p);
         p=p->leftchild;
     }
     if(!s.empty())
     {
         Tree tmp=s.top();
         s.pop();
         p=tmp->rightchild;

         cout<<tmp->data<<"";
     }
 }
}

后续遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/*仿照前序遍历的思路，实现根右左，再利用t栈反向输出为左右根*/
void Suctraverse(Tree&tree)
{
 stack<Tree>s,t;
 Tree p=tree;
 while(!s.empty()||p!=NULL)
 {
     while(p!=NULL)
     {
         t.push(p);

         s.push(p);
         p=p->rightchild;

     }
     if(!s.empty())
     {
         Tree tmp=s.top();
         s.pop();
         p=tmp->leftchild;
     }
 }
 while(!t.empty())
 {
     Tree tmp=t.top();
     t.pop();
     cout<<tmp->data<<"";
 }
}

层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/*层序遍历*/
void LevelTravel(Node* tree)
{
  if(tree == nullptr) {
      return;
}

queue<Node*> Q;
Q.push(tree);

while(!Q.empty())
{
  Node* q = Q.front();
  cout << q->data << " ";
  Q.pop();

  if (q->lchild) {
      Q.push(q->lchild);
  }
  if (q->rchild) {
      Q.push(q->rchild);
  }
}
}

树的计算

树整体结点个数的计算

1
2
3
4
5
6
7
8
9
10
11
12
13
/*统计结点个数*/
int GetNum(BiTree&tree)
{
  if(tree==NULL)
  {
      return 0;
  }
  int lheight=GetNum(tree->lchild);
  int rheight=GetNum(tree->rchild);

  return lheight+rheight+1;
}

树整体深度的计算

1
2
3
4
5
6
7
8
9
10
11
12
/*树的高度*/
int GetHeight(BiTree&tree)
{
  if(tree==NULL)
  {
      return 0;
  }
  int lheight=GetHeight(tree->lchild);
  int rheight=GetHeight(tree->rchild);

  return max(lheight,rheight)+1;
}

计算树的宽度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int TreeWidth(Tree tree)
{
     if (tree == NULL) {
         return 0;
     }
     int maxWidth = 1; // 记录当前最大宽度
     queue<Tree> q;
     q.push(tree);

     while (!q.empty()) {
         int levelSize = q.size(); // 当前层的节点个数
         for (int i = 0; i < levelSize; i++) {
             Tree node = q.front();
             q.pop();
             if (node->leftchild != NULL) {
                 q.push(node->leftchild);
             }
             if (node->rightchild != NULL) {
                 q.push(node->rightchild);
             }
         }
         if (q.size() > maxWidth) {
             maxWidth = q.size();
         }
     }
     return maxWidth;
}

树的高级玩法

判断一棵树是否为完全二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/*判断是否为完全二叉树*/
bool isCompleteBinaryTree(BiTree&tree) {
  if (!tree) {
      return true;
  }

  std::queue<Node*> q;
  q.push(tree);

  while (!q.empty()) 
  {
      Node* current = q.front();
      q.pop();

      if (!current) //如果层序遍历过程中出现了空
      {
          while (!q.empty()) //需要检验后续遍历所有的结点是否都为空，否则就return false
          {
              Node* temp = q.front();
              q.pop();
              if (temp) 
              {
                  return false;
              }
          }
          return true;
      }
      q.push(current->lchild);
      q.push(current->rchild);
  }
  return true;
}

根据前序与中序遍历还原二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/*前序中序还原二叉树*/
BiTree PreInTree(const char *pre,const char *mid,int x)
{
  if(x<=0) return NULL;//如果root==-1，无论左子树还是右子树都不会继续递归

  BiTree t=new Node;
  t->data=*pre;
  int root=-1;

  for(int i=0;i<x;i++){
      if(mid[i]==*pre){
          root=i;//找到中序遍历中“中点”的位置
          break;
      }
  }
  t->lchild=PreInTree(pre+1,mid,root);//在中序的左半边找左孩子
  t->rchild=PreInTree(pre+1+root,mid+1+root,x-root-1);//在中序的右半边找右孩子，初始下标为mid+1+root，查找范围是这个下标后的x-root-1个数据
  return t;
}

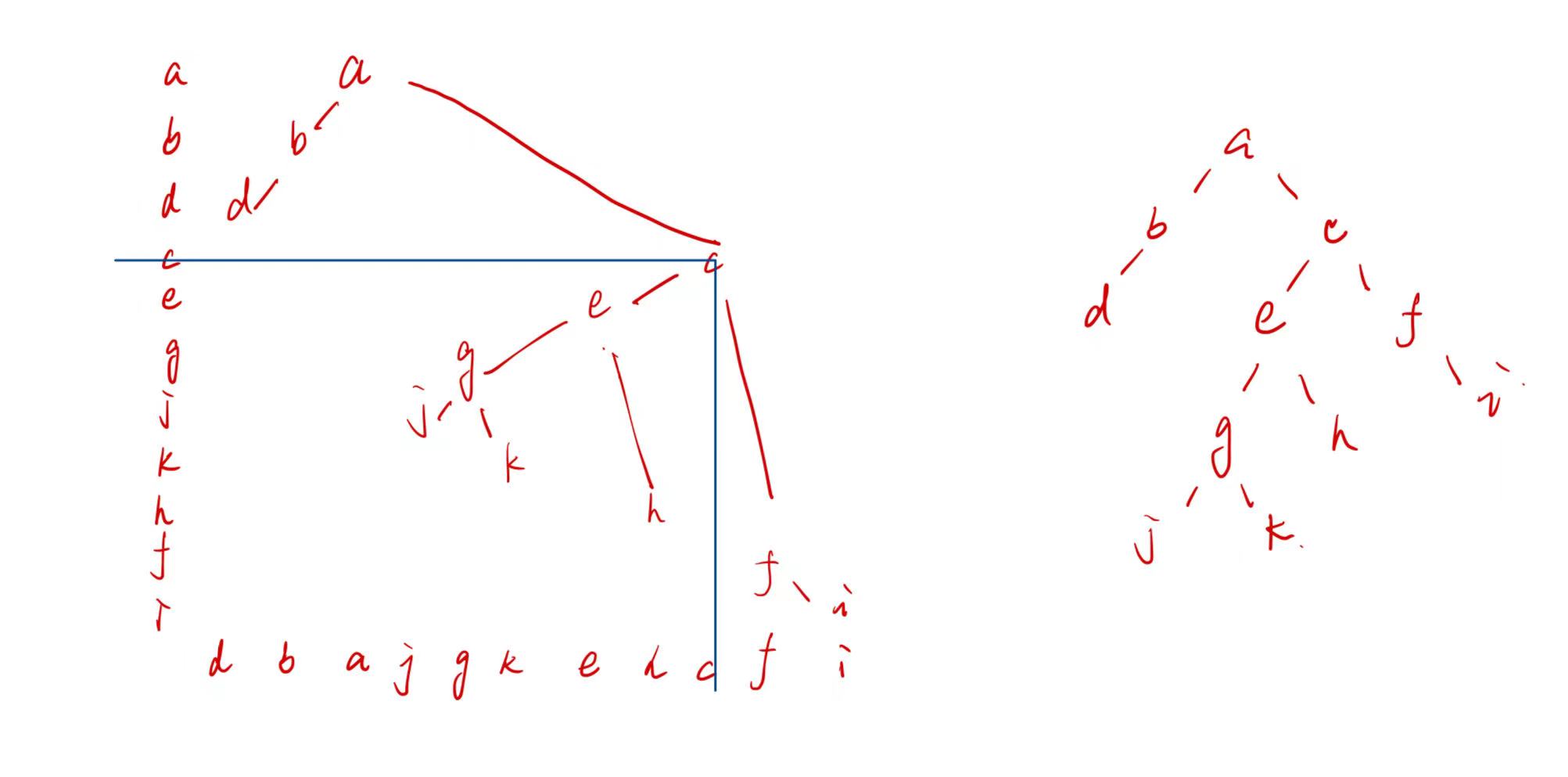
网格法前序中序还原二叉树

x轴写中序，y轴写前序遍历。

img

N叉树转化为二叉树

兄弟结点之间连线，去除父亲结点与长子之外的连线。

森林转化为二叉树

将所有N叉树转化为二叉树，再将二叉树之间以父亲结点与右孩子的方式连接

二叉树转化为树

父亲结点与左孩子的右孩子连线，去除左孩子与右孩子的连线。

二叉树转化为森林

断开所有父节点与右孩子的连线，再由二叉树转化为树

哈夫曼树的理解

img

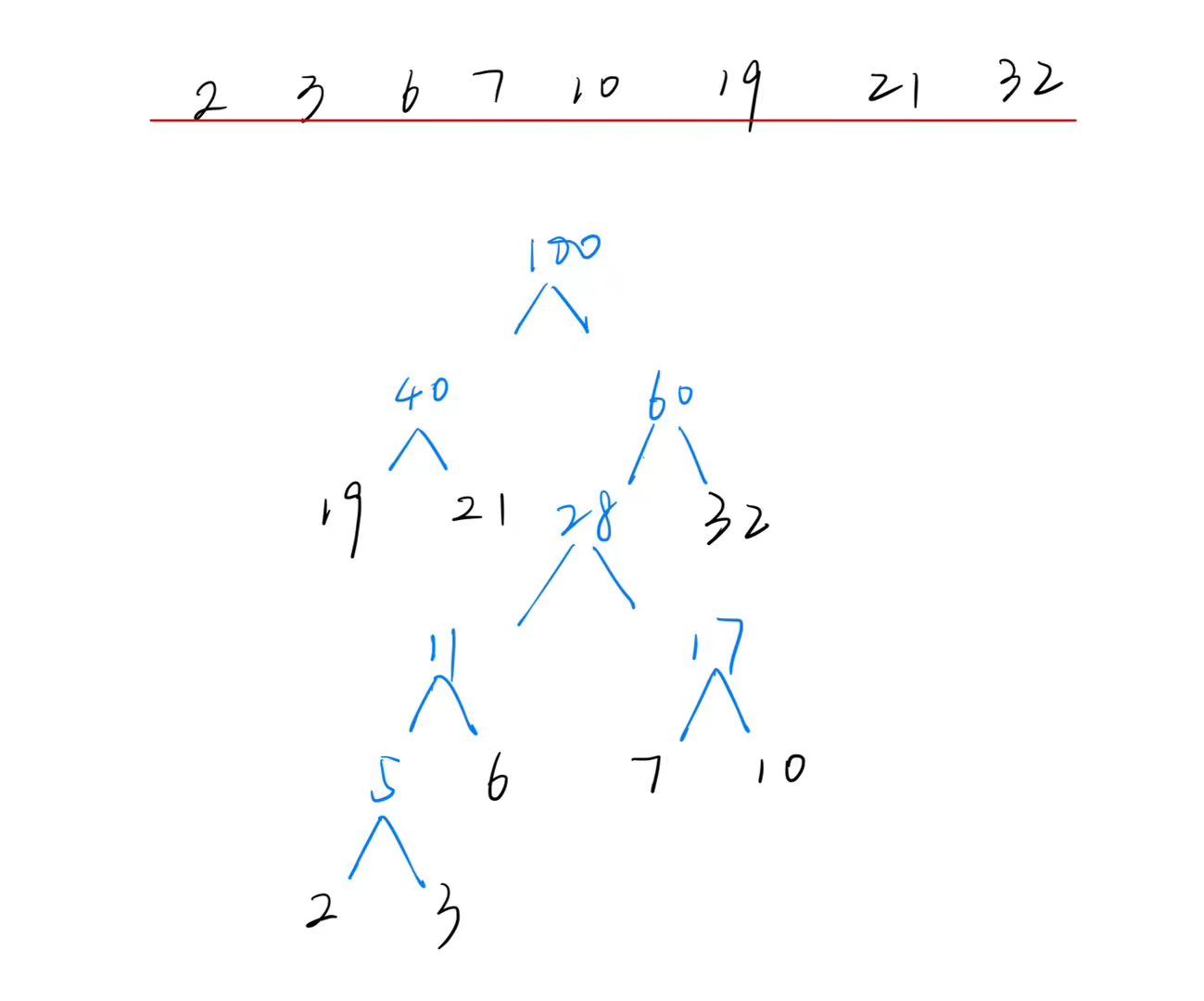
图

邻接矩阵遍历

MartrixDFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 以顶点v0为起点，进行一趟DFS
void DFS(const Graph& G, int v0, int visited[]){
  // 第一步： 先访问v0，标记已访问
 visited[v0]=1;
 cout<<v0<<" ";
 // 第二步： 再对v0的所有未被访问的邻接点进行DFS
  for(int j=0;j<G.vexNumber;j++)
  {
       if(G.adjMatrix[v0][j]&&!visited[j])
      {
          DFS(G,j,visited);
         }
    }
}
// 对整个图进行DFS
void DFS(const Graph& G){
   // 第一步：初始化visited数组
  int visited[1000];
    for(int i =0;i<G.vexNumber;i++){
      visited[i]=0;
    }
     // 第二步：以每个未被遍历的顶点为起点，进行DFS
     for(int i =0;i<G.vexNumber;i++){
         if(visited[i]==1)
         {
             continue;
         }
         else{
             DFS(G,i,visited);
       }
     }
}

MartrixBFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/*对整个图进行BFS*/
void BFS(const Graph& G){
    // 第一步：初始化visited数组
    int visited[1000];
    for(int i =0;i<G.vexNumber;i++){
         visited[i]=0;
     }
     // 第二步: 挨个挑结点作为起点遍历整个图
    for(int i =0;i<G.vexNumber;i++){
    if(visited[i]==1)
    {
        continue;
     }

      visited[i]=1;
      cout<<i<<" ";
      q.push(i);

      	while(!q.empty())
         {
             int x=q.front();
             q.pop();

               //按选定结点继续BFS发散
              for(int j=0;j<G.vexNumber;j++)
              {
                 if(G.adjMatrix[x][j]&&!visited[j])
                  {
                     visited[j]=1;
                      cout<<j<<" ";
                      q.push(j);
                   }
           }
       }
  }
}

连通分量问题

Finished序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void FinishDFS(const Graph& G, int v0, int visited[]){
	visited[v0]=1;

	for(int j=0;j<G.vexNumber;j++)
 {
     if(G.adjMatrix[v0][j]&&!visited[j])
     {
         DFS(G,j,visited);
     }
 }
 cout<<v0<<" ";//每次遍历结果都与深度遍历反向输出
}
// 对整个图进行DFS
void FinishDFS(const Graph& G){
int visited[1000];
 for(int i =0;i<G.vexNumber;i++){
   visited[i]=0;
 }
  for(int i =0;i<G.vexNumber;i++){
      if(visited[i]==1)
      {
          continue;
      }
      else{
          DFS(G,i,visited);
    }
  }
}

拓扑排序

判断是否是有效拓扑序列：

计算每个结点的入度，按照入度为0的结点开始检测，删除结点出度。

最早发生时间：

每个结点在全部前面限制要素都被满足后，最早开始的时间（加上前面结点的最大值，使之自身最大）

最迟发生时间：

从终点开始倒推，计算前面结点的的最迟发生时间，否则就会影响最终结果（减去后面结点的最大值，使得自身最小）

最早工期问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void CalculateVl(Graph &g,int outDegree[])
{
 stack<int> s;
 int max=0;
 for(int i=0;i<g.nodeNumber;i++)
 {
     if(max<g.ve[i]) max=g.ve[i];
 }
 for(int i=0;i<g.nodeNumber;i++){
     g.vl[i]=max;
     if(outDegree[i]==0)
     s.push(i);
 }
 while(!s.empty()){
     int q=s.top();
     s.pop();
     for(int i=0;i<g.nodeNumber;i++)
     {
         if(g.adjMatrix[i][q]==1)
         { 
             outDegree[i]--;
             if(g.vl[i]>g.vl[q]-g.weight[i][q])
             g.vl[i]=g.vl[q]-g.weight[i][q];

             if(outDegree[i]==0) s.push(i);
         }
     }
 }
}

最终取所有结点的最早发生时间就是最短工期。

最小生成树

最小生成树

生成树的概念：一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。（再加一条边就会出现回路）

最小生成树：边的权重之和最小

MST性质

设无向图G=(V, E)，U 是顶点集V的一个非空子集。若（u , v ）是一条具有最小权值（代价）的边，其中u∈U， v∈V - U，则必存在一棵包含边（u，v）的最小生成树

Prim算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
void MSTprim(GraphMatrix&graph)
{
int num=graph.NumVertex;
int cost[200];
int adj[200];//已经纳入路径的结点到达其余结点的距离
int totalcost=0;
cost[0]=-1;
adj[0]=0;

//初始化cost数组
for(int i=1;i<num;i++)
{
   cost[i]=graph.edge[0][i];
   adj[i]=0;
}

//每次取一个顶点
for(int i=1;i<num;i++)
{
   int k=0;
   int minicost=999;

   //【找最小】：找到目前所有连接点中最小的那个
   for(int j=1;j<num;j++)
   {
       if(cost[j]>0&&cost[j]<minicost)
       {
           minicost=cost[j];
           k=j;
       }
   }

   //成功加入最小的那个
   cout<<"minicost"<<i<<": "<<minicost<<endl;
   totalcost+=minicost;
   cost[k]=-1;

   //【做替换】：在新加入的范围内去更新所有点的连接，看看有没有多出来更短的路线
   for(int j=1;j<num;j++)
   {
       if(graph.edge[k][j]<cost[j]&&graph.edge[k][j]!=0&&cost[j]>0)//之前可达的结点有更优路径
       {
           cost[j]=graph.edge[k][j];
           adj[j]=k;
       }
       if(graph.edge[k][j]!=0&&cost[j]==0)//之前不可达，加入了新节点可达
       {
           cost[j]=graph.edge[k][j];
           adj[j]=k;

       }
		}
}
cout<<"最小总权重";
cout<<totalcost<<endl;
}
/*测试用例，数组中的元素存在三种状态，第一种是已经cost=-1：表示该点已经在U之内，第二种是cost=0；表示该点不可达；第三种是cost>0，表示可达，有路径需要比较
0  10 9  13 0  0  0
10 0  0  15 7  0  12
9  0  0  4  0  3  0
13 15 4  0  0  22 23
0  7  0  0  0  0  20
0  0  3  22 0  0  32
0  12 0  23 20 32 0
*/

Kruskal算法

  • E1：将所有的边按权值排序；

  • E2：设每个顶点为一个独立的点集，生成树T为空集；

  • E3：依序扫描每一条边<vi,vj>，直到已输出n-1条边：

    • E31：若vi、vj不在同一点集中，则将该边加入生成树T中，并合并这两个点集；否则舍弃该边；

最短路径

DijKstra

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#include<bits/stdc++.h>
using namespace std;
#define INF 99999999
#define  MAX 50

typedef struct{
     int NumVertex;
     string vertex;
     int edge[MAX][MAX];
}GraphMatrix;

void Dijkstra(GraphMatrix&graph,int start)
{
     int finish[MAX];
     int shortest[MAX];

     //初始化
     for(int i=0;i<graph.NumVertex;i++){
         finish[i]=0;
         if(graph.edge[start][i]!=0)
      shortest[i]=graph.edge[start][i];
      else{
          shortest[i]=INF;
      }
     }
     //第一个结点
  finish[start]=1;
     for(int i=0;i<graph.NumVertex-1;i++){
         int min=100000;
         //找结点
         int k=-1;
         for(int j=0;j<graph.NumVertex;j++)
         {
             if(!finish[j]&&shortest[j]<min)
             {
                 min=shortest[j];
                 k=j;
             }
         }
         finish[k]=1;

         //更新shortest
         for(int j=0;j<graph.NumVertex;j++)
         {
             if(shortest[j]>shortest[k]+graph.edge[k][j]&&graph.edge[k][j]!=0)
             {
                 shortest[j]=shortest[k]+graph.edge[k][j];
             }
         }
 	}

  //输出到每个节点的最短路径
     for(int i=0;i<graph.NumVertex;i++){
         if(i!=start)
         {
             if(shortest[i]==INF)
                 cout<<"-1"<<" ";//不可达
             else{
                 cout<<shortest[i]<<" ";
             }
         }
      }
}

int main()
{
     GraphMatrix graph;
     int start;
     cin>>graph.NumVertex>>start;
     InputMatrixGraph(graph);
     Dijkstra(graph,start);
     return 0;
}

/*
0  10 9  13 0  0  0
10 0  0  15 7  0  12
9  0  0  4  0  3  0
13 15 4  0  0  22 23
0  7  0  0  0  0  20
0  0  3  22 0  0  32
0  12 0  23 20 32 0
*/
/*
4 1
0 3 0 1
0 0 4 0
2 0 0 0
0 0 1 0

6 4 7 
*/

FLOYD

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include<bits/stdc++.h>
using namespace std;
#define  MAXSIZE 100//此处的数字后面不需要加“ ; ”
#define INF 99999999

typedef struct{
int NumVertex;
string vertex;
int edge[MAXSIZE][MAXSIZE];
}GraphMatrix;

void Floyd(GraphMatrix&graph,int start)
{
int num=graph.NumVertex;
int path[200][200];//记录到该结点的结点
int shortest[200][200];//记录到该点的最短路径;

 for(int i=0;i<num;i++)
 {
     for(int j=0;j<num;j++)
  {
      if(graph.edge[i][j]==0)
      {
          path[i][j]=INF;
             shortest[i][j]=INF;
         }
         else{
             shortest[i][j]=graph.edge[i][j];
             path[i][j]=graph.edge[i][j];
         }
     }
 }

for(int k=0;k<num;k++)
{
  for(int i=0;i<num;i++)
     {
         for(int j=0;j<num;j++)
         {
          if(shortest[i][k]==INF||shortest[k][j]==INF)//不可达，故跳过
             {
                 continue;
             }
             if(shortest[i][k]+shortest[k][j]<shortest[i][j])
             {
                 shortest[i][j]=shortest[i][k]+shortest[k][j];
                 path[i][j]=k;
             }
         }
     }
 }
}

int main()
{
   GraphMatrix graph;
     InputMatrixGraph(graph);
     Floyd(graph,0);
     return 0;
}
/*
4
0 3 0 1
0 0 4 0
2 0 0 0
0 0 1 0

输出
0 3 2 1 
6 0 4 7 
2 5 0 3 
3 6 1 0 
*/

查找

概念

平均查找长度（Average Search Length）

ASL是衡量一个查找算法的重要性能指标。

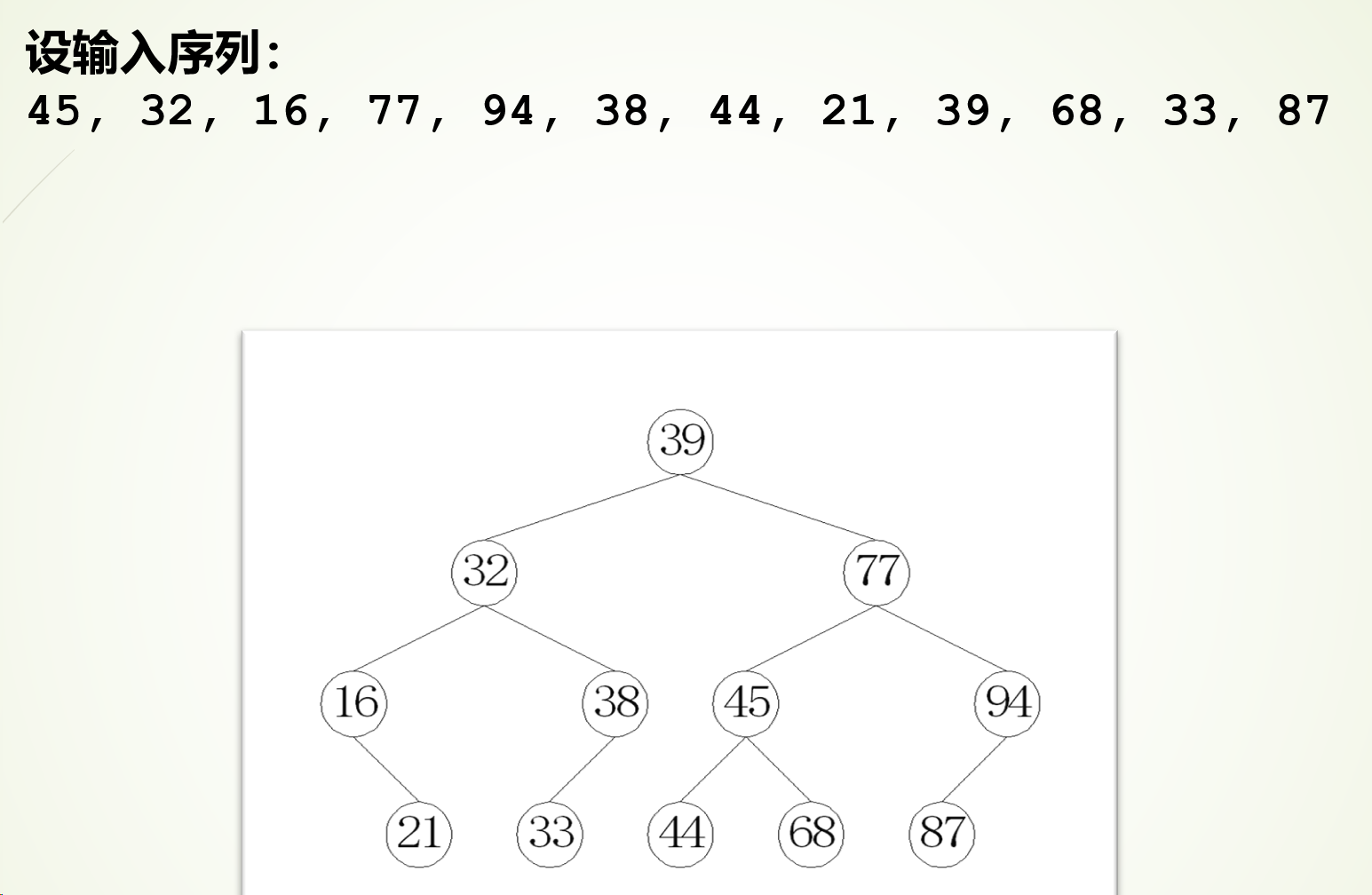
排序二叉树

ASL = logN

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/*排序二叉树的插入*/
void Insert(BiTree&tree,int x)
{
  if(tree==NULL)
  {
          tree=new BiNode;
          tree->data=x;
          tree->lchild=NULL;
          tree->rchild=NULL;
  }
  else if(x<tree->data)
  {
          Insert(tree->lchild,x);
  }
  else if(x>tree->data)
  {
          Insert(tree->rchild,x);
  }
}

void GetTree(BiTree&tree)
{
  int num;
  cin>>num;
  for(int i=0;i<num;i++)
  {
          int x;
          cin>>x;
          Insert(tree,x);
  }
}

排序二叉树的平衡因子计算：int BF=Height(*tree*->lchild)-Height(*tree*->rchild);

平衡二叉树

二叉排序树按照中序遍历是递增的。
结点插入

以不平衡二叉树的根节点开始，沿着新加入节点的方向，找与之相邻的三个结点

img

结点删除

①删除叶子结点：直接删去。

②删除结点仅含有左孩子或右孩子：用唯一的一个孩子替换删除的结点。

③删除结点同时包含左孩子右孩子：找到它的后继（中序遍历）将其替换。需要注意中序遍历别找错了。

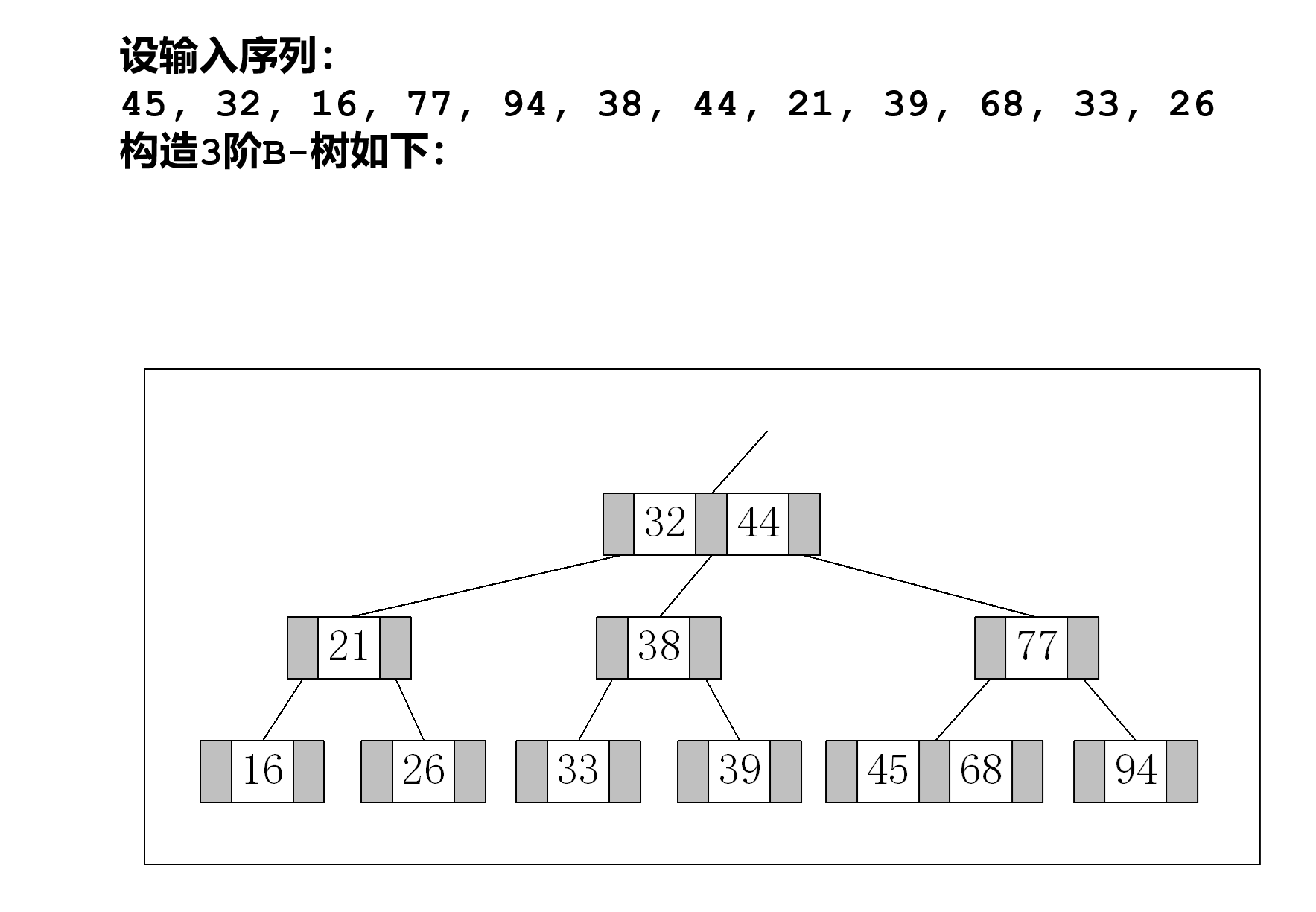
B-树

性质：

  • N阶-B树每个结点的数据量不超过N-1,

  • 非根结点至少有N/2（向下取整）个关键字。

  • 每个结点最多有N个分支。

分裂插入：

img

合并删除:

理解：父节点对其子结点负责

删除操作分为三种情况

  • 删除叶子结点数据，在叶子结点删除后依然维持>1=个关键字时候，直接删除。否则，需要对应父节点进行相应调整
  • 借兄弟节点删除，删除数据后，父节点调整。在兄弟结点满足关键字最小要求的情况下，兄弟结点需要补充上去一个关键字充当父亲结点；
  • 借不了兄弟结点，删除数据后，父节点调整。需要继续合并子节点。

img

哈希表

给定一个长度为10，标号为**[0..9]的存储表
给定一组关键字，你需要把这组数据以规定的方法放进存储表中
首先把关键字的后四位数字求和**，该和对10求模，然后按照求模结果，放进存储表中对应标号的位置。
（例如，求模结果是2，则这个关键字应该放在存储表中标号为2的位置）

但是，不同的关键字可能会产生相同的求模结果。

Hash表-线性探测法解决冲突
那么你需要在存储表中为较晚输入的关键字探测到一个空闲位置，该探测方法为标号+1、-1、+2、-2、+3、-3…
例如当前求模结果依然是2，但是标号为2的位置已经被占用了，那么首先对该求模结果+1得到3，如果标号为3的位置是空闲，则把该关键字放进标号为3的位置中。如果标号为3的位置依然被占用了或者不存在，则改为-1、+2、-2、+3、-3…以此类推。

Hash表-链表法解决冲突
注意在存储的链表表中，把较晚输入的关键字拼接在原来此处关键字的前面，用空格分隔。

ASL查找成功的平均查找长度

排序

简单排序

选择排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void chooseSort(int n,int*num)
{
 for(int i=0;i<n;i++)
 {
     int min=i;
     for(int j=i+1;j<n;j++)
     {
         if(num[i]>num[j])
         {
             min=j;
         }
     }

     int tmp=num[min];
     num[min]=num[i];
     num[i]=tmp;
 }
}

插入排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void insertionSort(int*num, int n) 
{
 for(int i=1;i<n;i++)
 {
     int key=num[i];//取需要插入的数据作为key值
     int j=i-1;
     while(num[j]>key&&j>=0)//把比key值小的数据往后覆盖，腾出恰当的位置放置key
     {
         num[j+1]=num[j];
         j=j-1;
     }
     num[j+1]=key;
 }
}

高级排序算法

快速排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
using namespace std;

/*最重要的是先去一个mid值作为比较，把整个数组划分为比mid大和比mid小的连块部分*/
int Partition(int s,int t,int*num){
 int mid=num[s];
 while(s<t)
 {
     while(s<t)
     {
         if(num[t]<mid)
         {
             num[s]=num[t];
             break;//容易落下
         }
         t--;
     }
     while(s<t)
     {
         if(num[s]>mid)
         {
             num[t]=num[s];
             break;
         }
         s++;
     }

 }
 num[s]=mid;
 return s;

}

void QuickSort(int s,int t,int*num){
 if(s<t){//容易忘截止条件
 int pivot=Partition(s,t,num);
 QuickSort(s,pivot-1,num);
 QuickSort(pivot+1,t,num);
 }
}
归并排序

类比有序表合并过程。

堆排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/*调整*/
//传参中的n是需要调整的大小，s是需要调整的起点
int HeapAdjust(int L[], int n, int s)
{
    // 从指定起点调整到叶结点（没有左子即为叶结点）
    int i = s;
    while (2*i+ 1< n)
    {
        // 确定结点i的最大子结点j
        int j =2*i+ 1;
        if (j + 1 < n && L[j] < L[j + 1]) 
            j++;
        if (L[j] <= L[i]) 
            break;   
        swap(L[j], L[i]);
        i = j;
    }
    return 0;
}

/*建堆*/
int CreateHeap(int L[], int n)
{
    for (int i = n / 2 - 1; i >= 0; i--)
    {
        HeapAdjust(L, n, i);
    }
    return 0;
}

/*堆排序*/
int HeapSort(int L[], int n)
{
    // 先将待排序序列创建成一个大顶堆
    CreateHeap(L, n);

    // 开始排序，待处理的大顶堆的结点数从n递减到1
    for (int i = n; i > 1; i--)
    {
        // 交换堆顶与最后一片叶子
        swap(L[0], L[i - 1]);

        // 调整
        HeapAdjust(L, i - 1, 0);
    }
    return 0;
}

性能分析

时间复杂度 瓶颈时间复杂度 空间复杂度 稳定性 要点
冒泡排序 O(n2) O(n2) O(1) 稳定 交换
选择排序 O(n2) O(n2) O(1) 不稳定 选择最小值
插入排序 O(n2) O(n2) O(1) 稳定 线性表的遍历
快速排序 O(nlogn) O(n2) O(logn) 不稳定 划分
堆排序 O(nlogn) O(nlogn) O(1) 不稳定 堆化/调整
归并排序 O(nlogn) O(nlogn) O(n) 稳定 有序表归并

思考题

对长度为N的无序序列，如何用不多于3N/2次比较找出最大和最小值？

任取一个标准,找到最大值和最小值。

  • 先对存储结构相邻两个数据进行比较，这个过程是N/2。
  • 再取较小的数据与最小值比较，统共需要比较N/2；取较大的数据与最大值比较，统共需要比较N/2。

中位数问题：用O(n)的平均时间复杂度从无序序列中找出第k大的元素。

利用快速排序分治思想

对序列L做划分，设划分位置的下标为i，则在数组中的排序rank=i-s+1;

若rank=k，则找到;

若rank<k，则在L[i+1]~L[n-1]中继续查找

若rank>k，则在L[0]~L[i-1]中继续查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int QuickSelect(int s, int t, int* num, int k) {
    if (s == t) {
        return num[s];
    }
    int pivot = Partition(s, t, num);
    int rank = pivot - s + 1;
    if (rank == k) {
        return num[pivot];
    } else if (rank > k) {
        return QuickSelect(s, pivot - 1, num, k);
    } else {
        return QuickSelect(pivot + 1, t, num, k - rank);
    }
}

细节

const常量引用

当传参的函数以const的形式传入时，说明数据不可以修改。只可以拷贝。

例如：传递进来的 list 参数是一个常量引用，因此不能直接对其进行修改。然而，在函数中直接修改了 list 中每个元素的值。

修改方法是：创建一个新的 List 结构体，然后将输入的 list 复制到新的结构体中，并且在新的结构体上进行修改。在最后将修改后的 List 结构体返回，而不是修改输入的 list 结构体本身。

while(cur)

在某些情况下，两者的使用会产生不同的效果。对于一些编译器而言，NULL 可能被定义为 0，因此 while(!cur) 可能被视为 while(cur == 0)，而这在语义上并不是一样的。因此，建议使用 while(cur != NULL) 来明确表达代码意图，代码更加清晰易懂。

memset

函数可以用来将一块内存区域的值全部设置为特定的值。通常情况下，我们可以使用memset将数组的所有元素初始化为0。以下是一个使用memset函数将数组初始化为0的示例代码:

1
2
int arr[5];
memset(arr, 0, sizeof(arr));